문제
피보나치 수열에 대한 정의가 다음과 같이 재귀적으로 주어졌다고 하자.
f(0) = f(1) = 1
f(n) = (f(n-1) + f(n-2)) % 1,000,000, for all 2 <= n <= 2^32.
위 피보나치 수열의 n번째 항인 f(n)을 출력하려고 한다.
Input
첫 번째 줄에 테스트 케이스의 개수 T가 주어진다.
두 번째 줄부터 한 줄에 하나씩 T개의 숫자 n이 주어진다.
입력값은 항상 정렬된 순서라고 가정해도 된다.
Output
각 테스트 케이스별로 한 줄에 하나씩 주어진 숫자 n의 피보나치 수열의 항 f(n)을 출력한다.
Sample Input1
10
0
1
2
3
4
5
6
7
8
9
Sample Output1
1
1
2
3
5
8
13
21
34
55
Sample Input2
5
100
1000
10000
100000
1000000
Sample Output2
84101
403501
597501
537501
937501
시간 복잡도 - Iterative(반복) 알고리즘을 사용해야 한다. (Recursive(재귀)보다 더 효율적임)
공간 복잡도 - 메모리를 효율적으로 사용하기 위해선 배열을 사용해서는 안된다.
이 문제에는 피사노 주기(Pisano Period)가 사용된다.
피사노 주기는 피보나치 수를 K로 나눴을 때 그 나머지가 항상 주기를 가지는 것을 말한다.
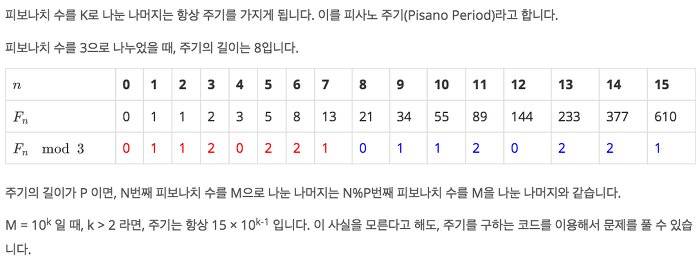
위 공식에 따르면 본 문제에서는 1000000으로 나눈 값을 값을 구하고 있으니
피사노 주기는 1500000이다.
따라, 피보나치 항을 구하는 fib() 함수를 구현할 때, b값을 그냥 리턴하지 않고 b%1000000해서 리턴해주고,
fib() 함수에 인자를 전달할 때는 피사노 주기인 1500000로 나눈 나머지 값을 넣어준다.
즉, n번 째 항인 f(n)을 구한다면 fib(n%1500000)을 계산하는 것이다.
또, fib()함수에서는 기존의 계산된 두 수 a,b와 임시 변수 temp 를 사용하여
값을 계속 갱신하는(?) 방식으로 코드를 구현하여
가장 큰 수까지 값을 한 번에 계산할 수 있도록 하였다.

<코드>
#include <stdio.h>
#define _CRT_SECURE_NO_WARNINGS
#define MAX 1500000
long long a, b, temp;
long long arr[MAX];
long long fib(long long n) {
a = b = 1;
for (int i = 2; i <= n; i++) {
temp = b;
b = a + b;
a = temp;
b %= 1000000;
}
return b;
}
int main() {
long long t, m;
scanf_s("%lld", &t);
for (int i = 0; i < t; i++) {
scanf_s("%lld", &m);
printf("%lld\n", fib(m % 1500000));
}
return 0;
}
<실행 결과>
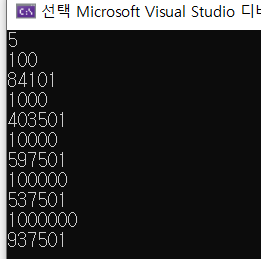
'Algorithm > 알고리즘' 카테고리의 다른 글
| [Python] set 연산 (0) | 2023.01.07 |
|---|---|
| [Python] 문자열에서 find 함수 (0) | 2023.01.01 |
| [백준 1929번] set 정렬 (0) | 2022.11.27 |
| [Python] DFS, BFS (0) | 2022.10.02 |
| 차대값과 차소값 찾기 (0) | 2021.03.26 |
